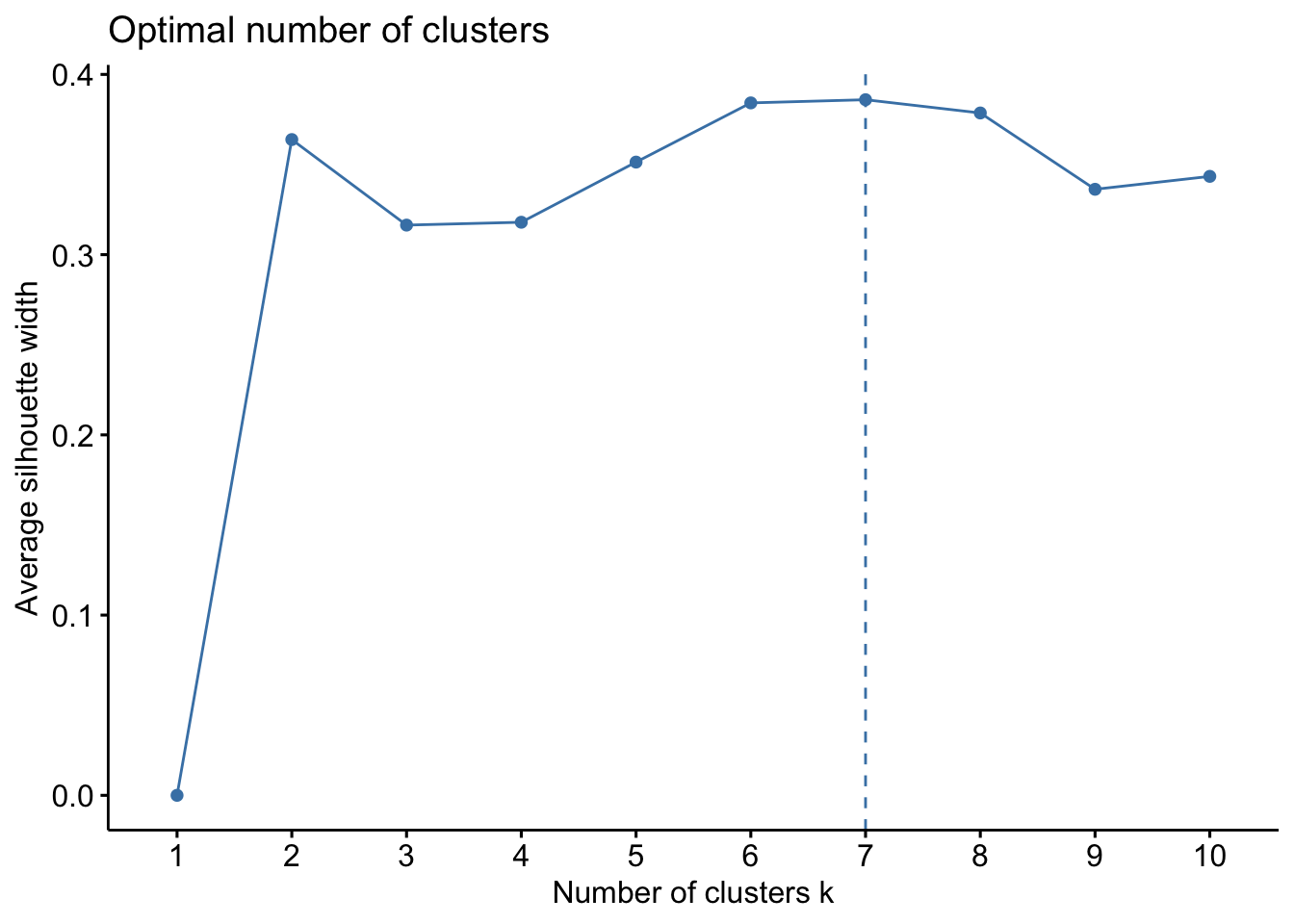
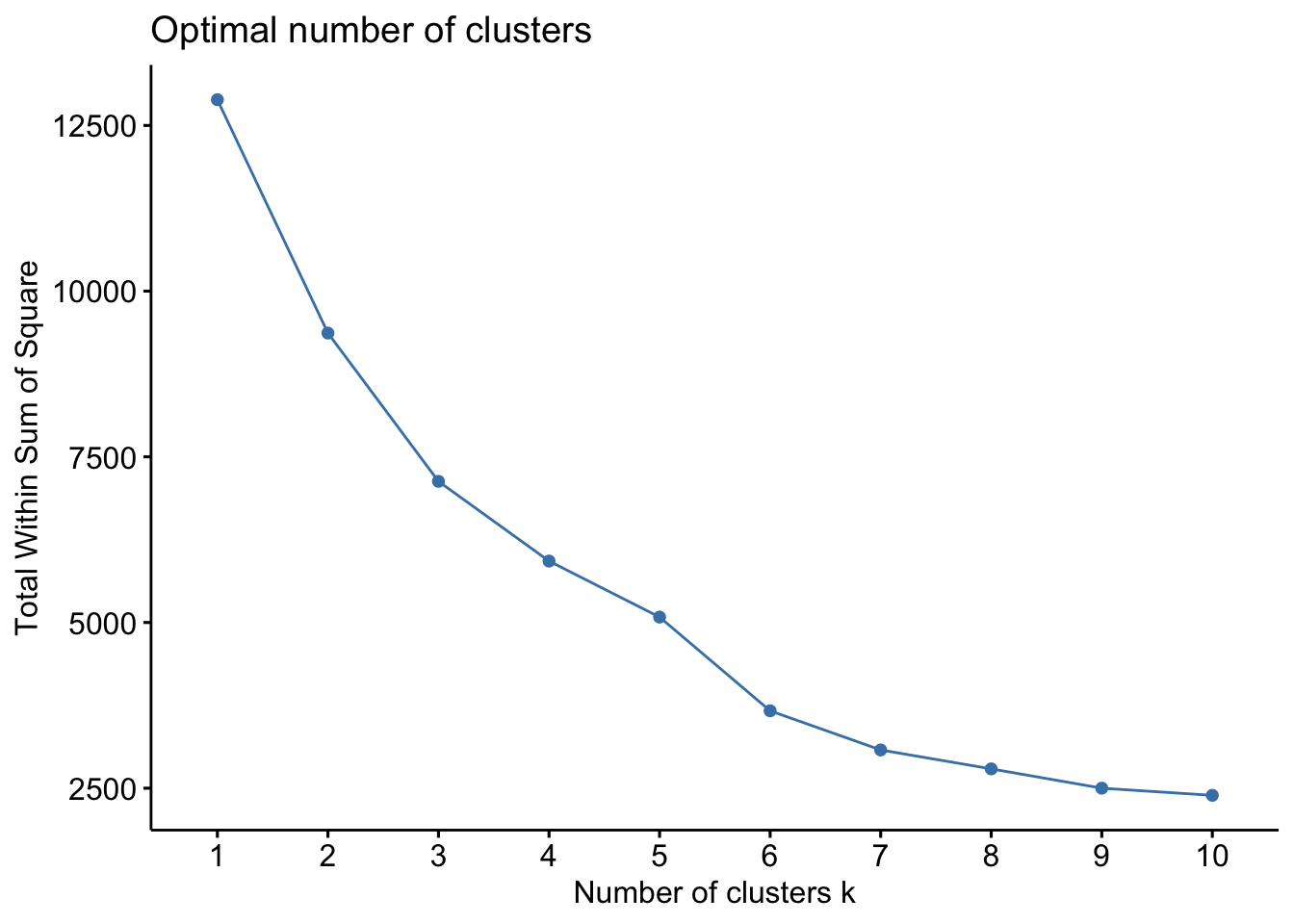
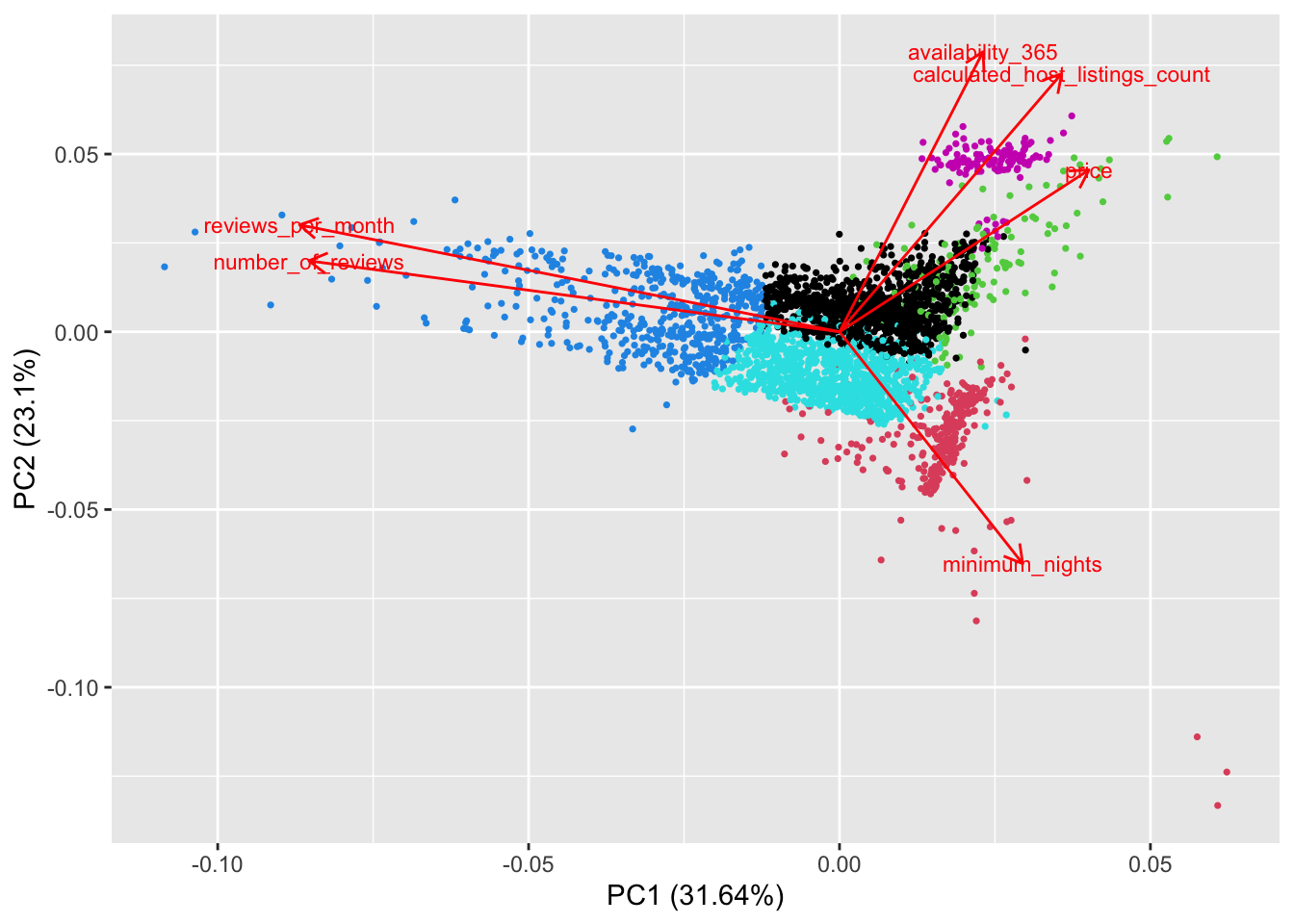
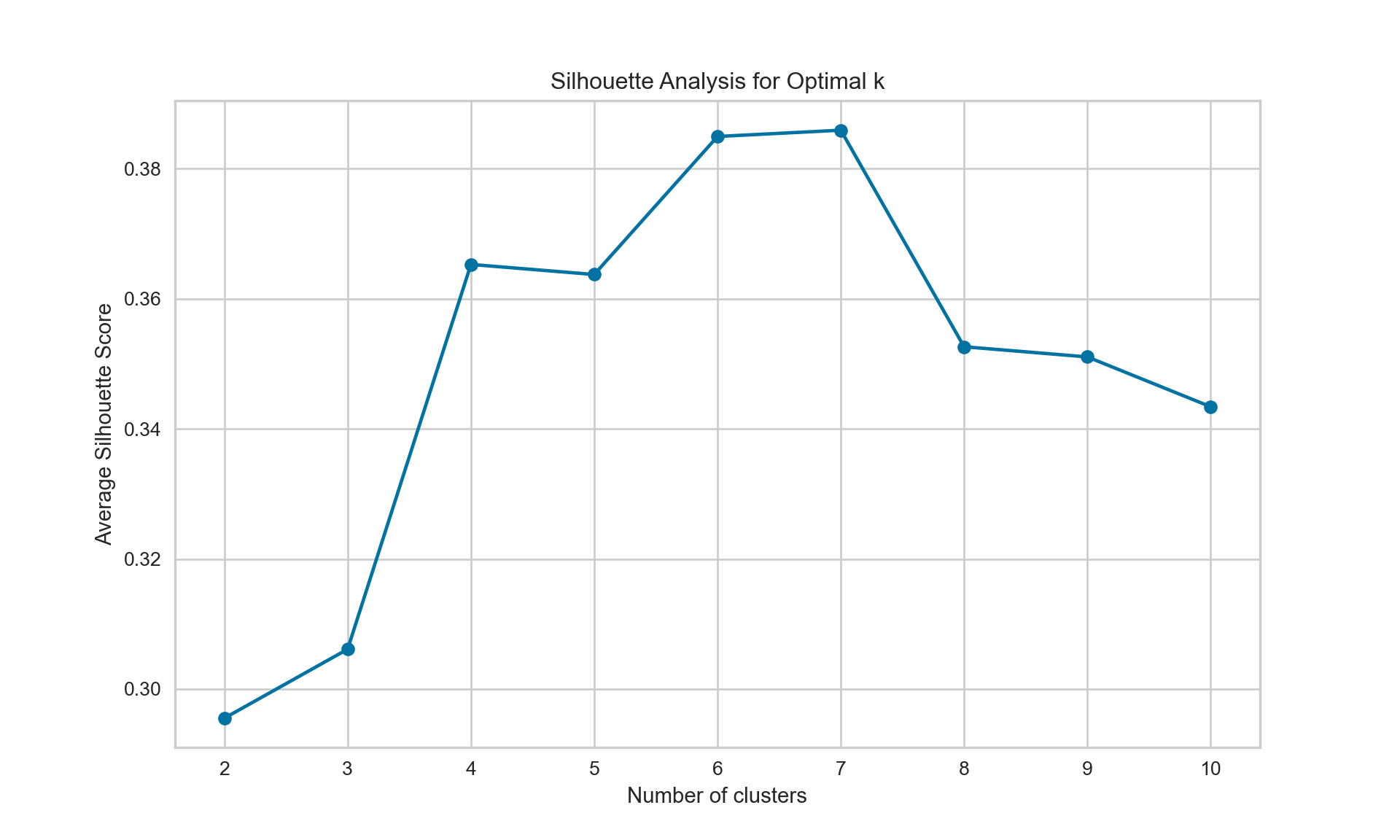
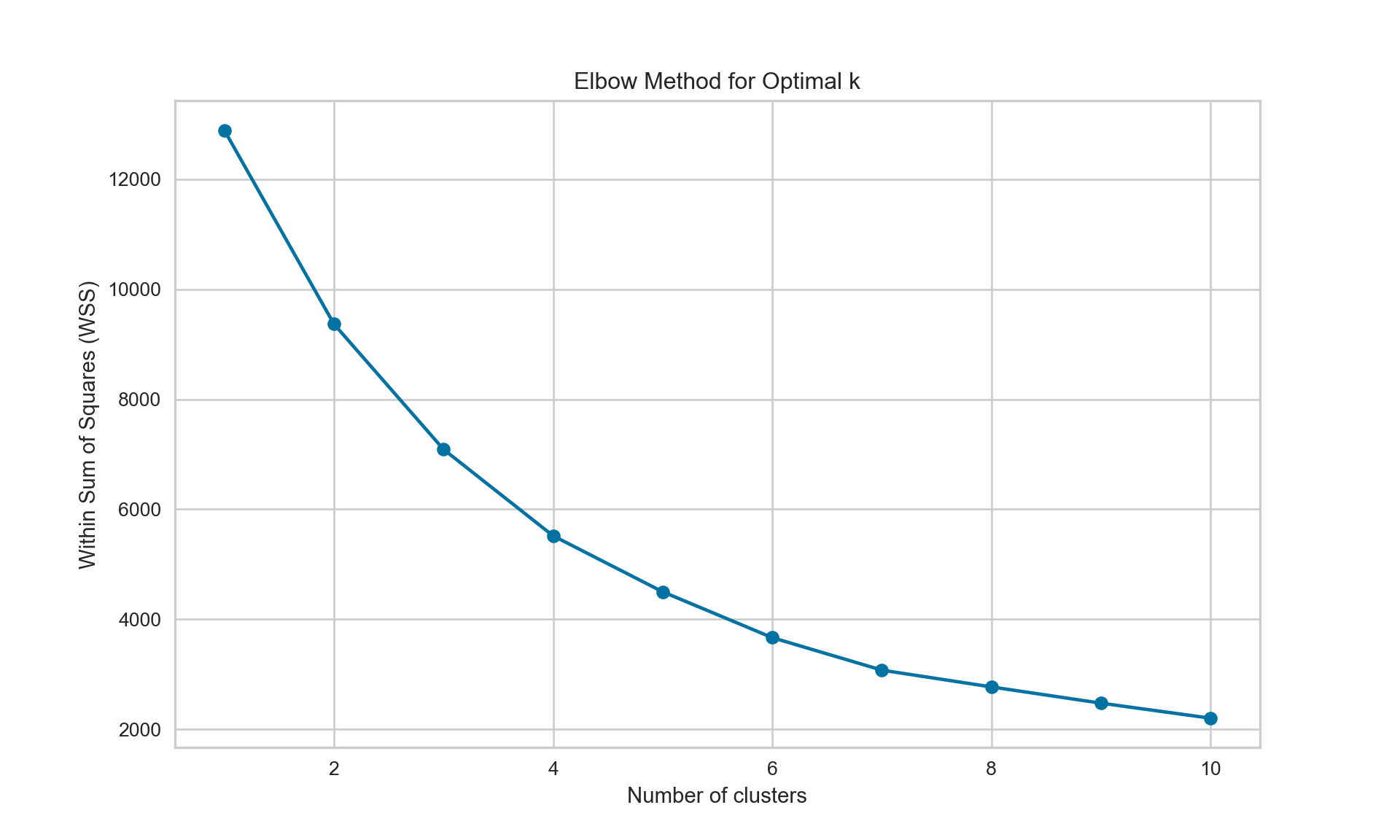
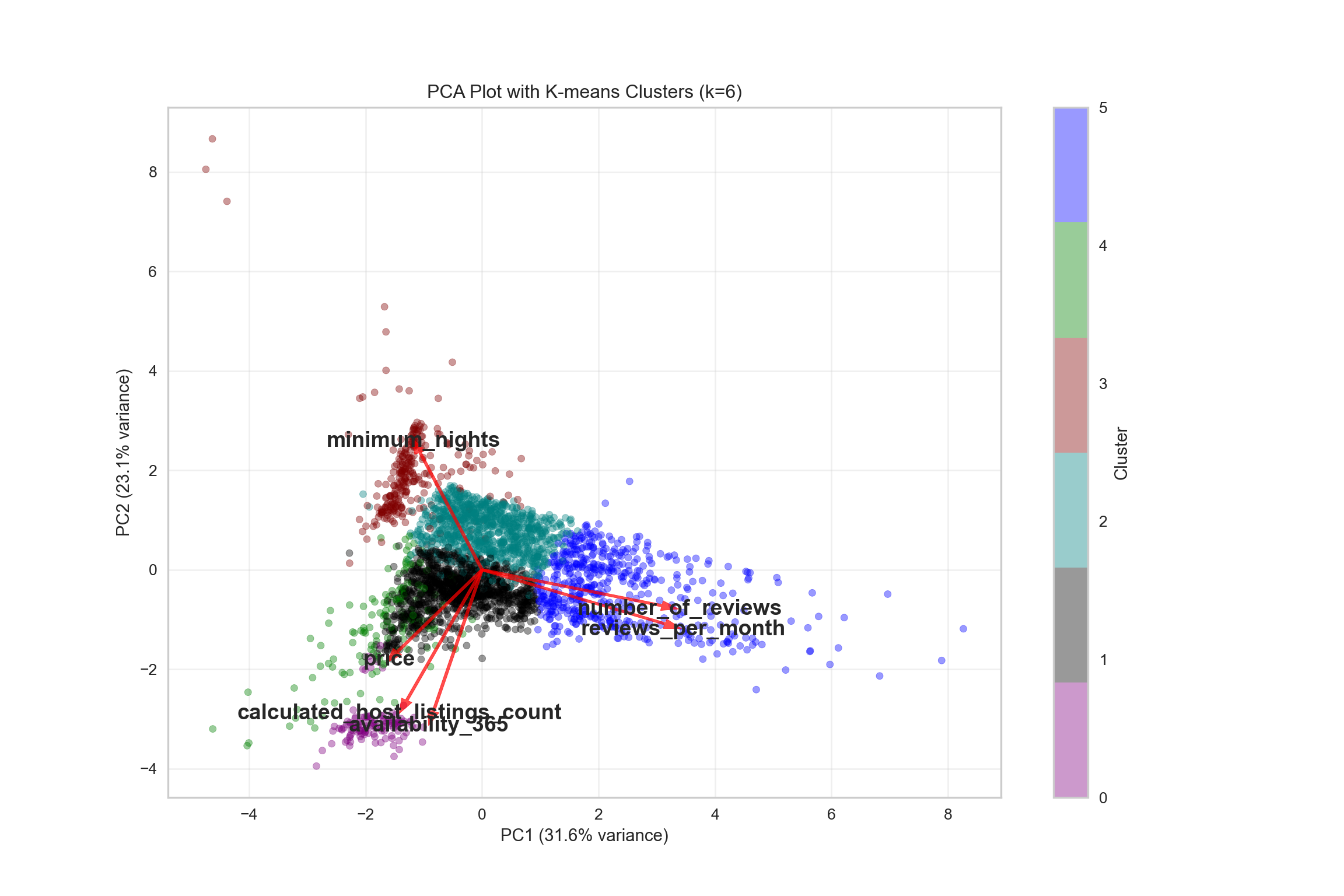
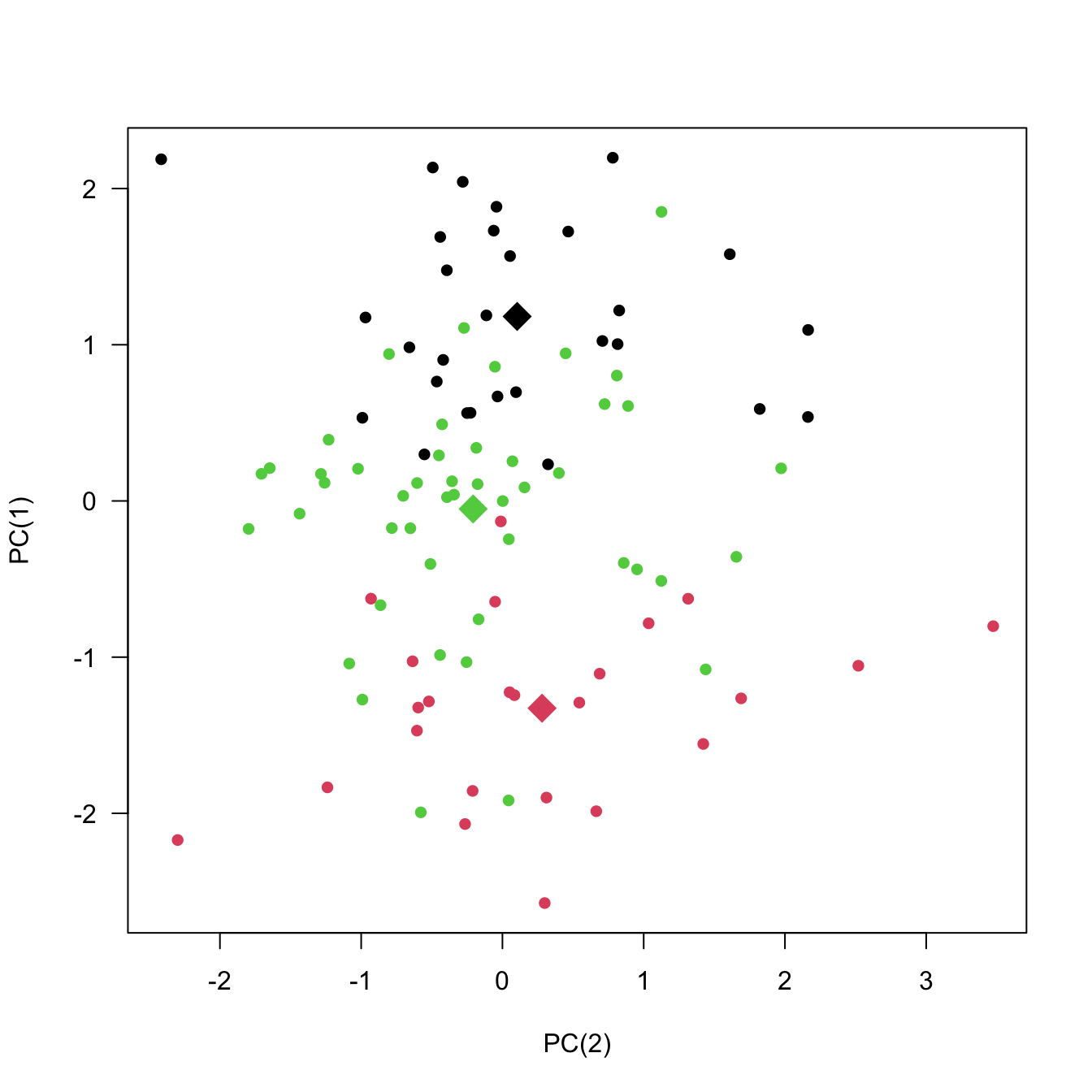
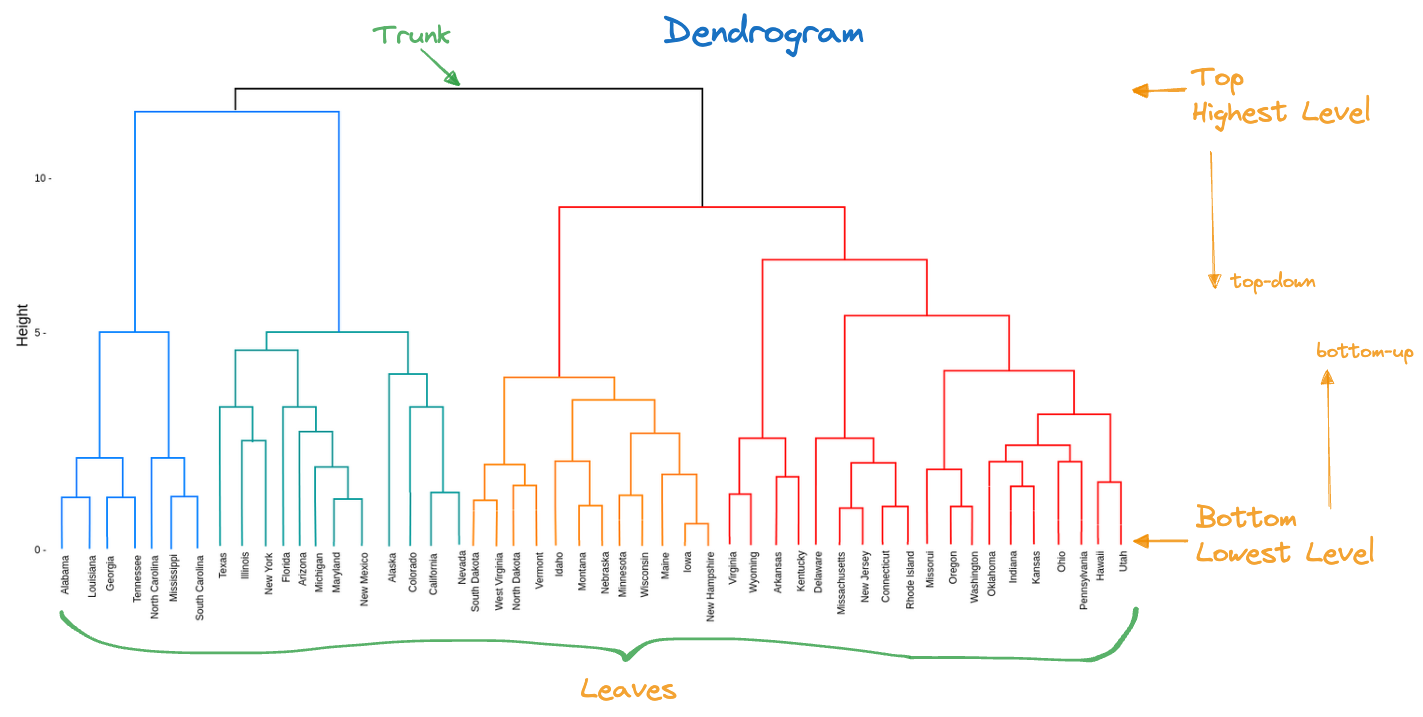
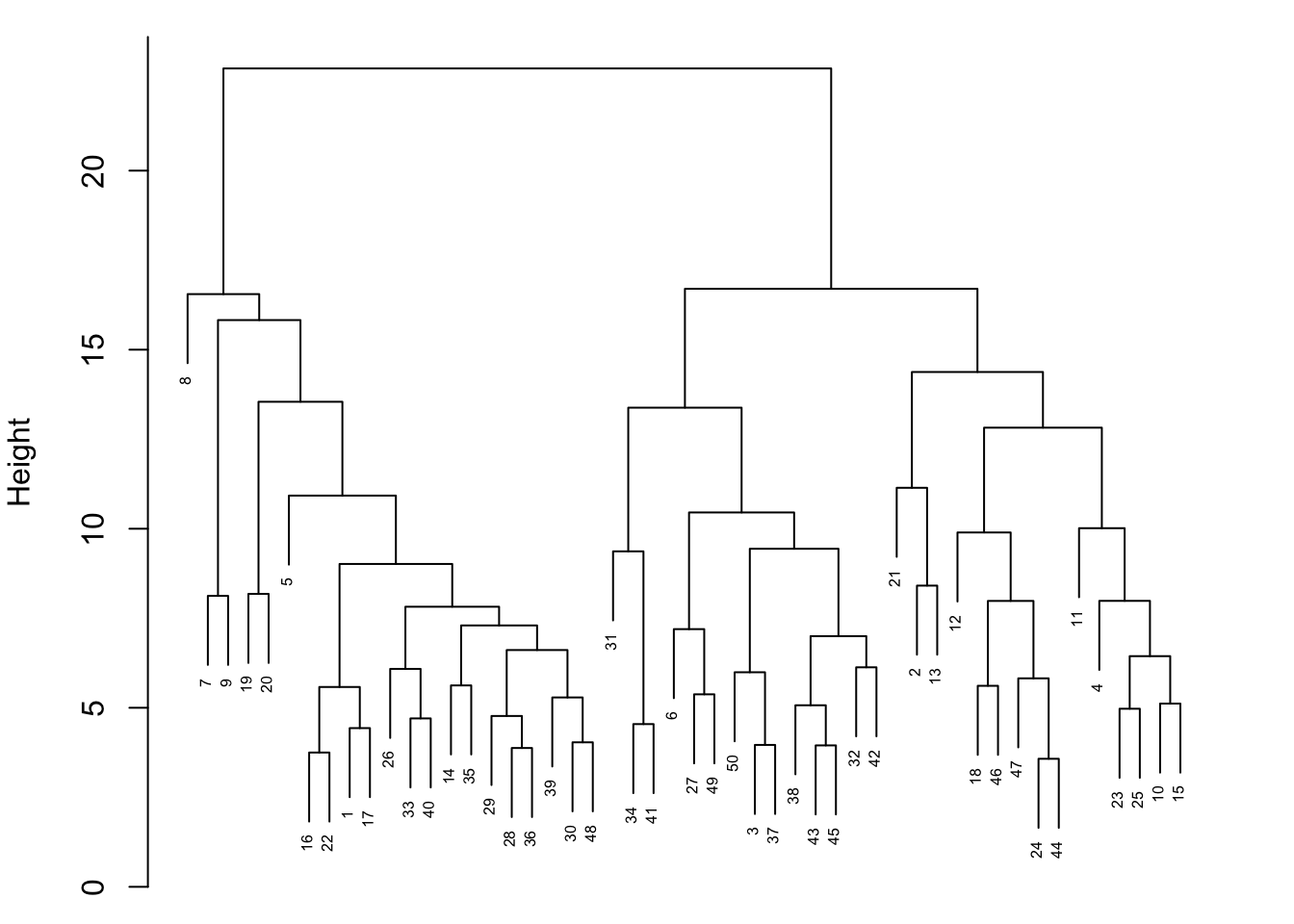
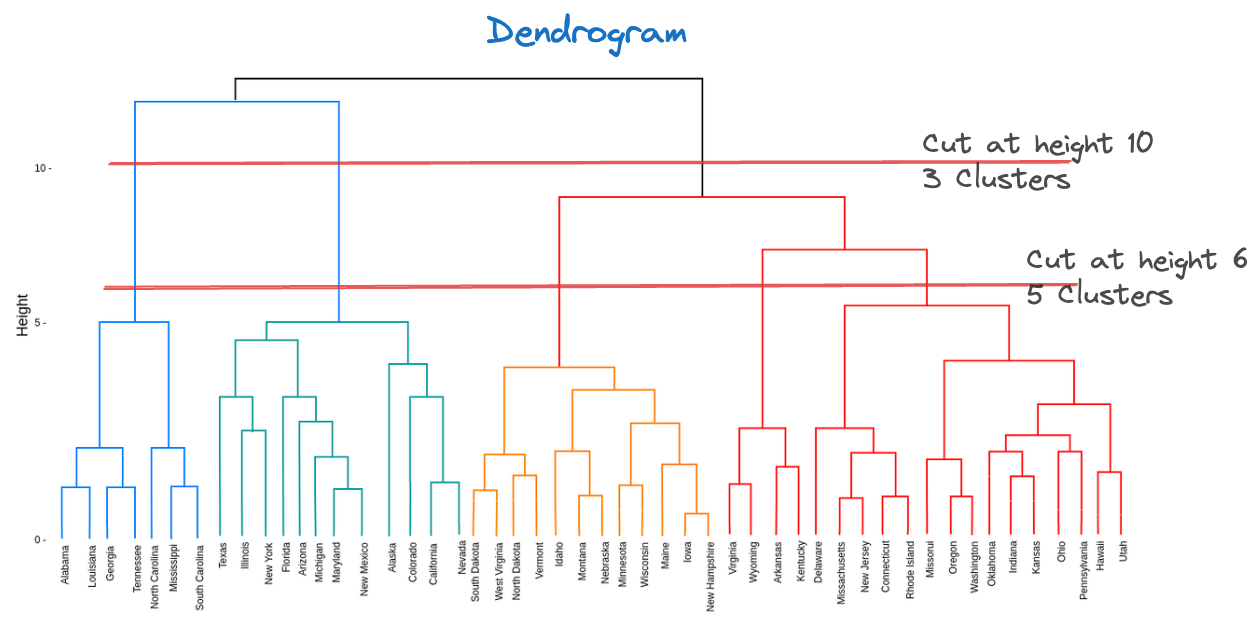
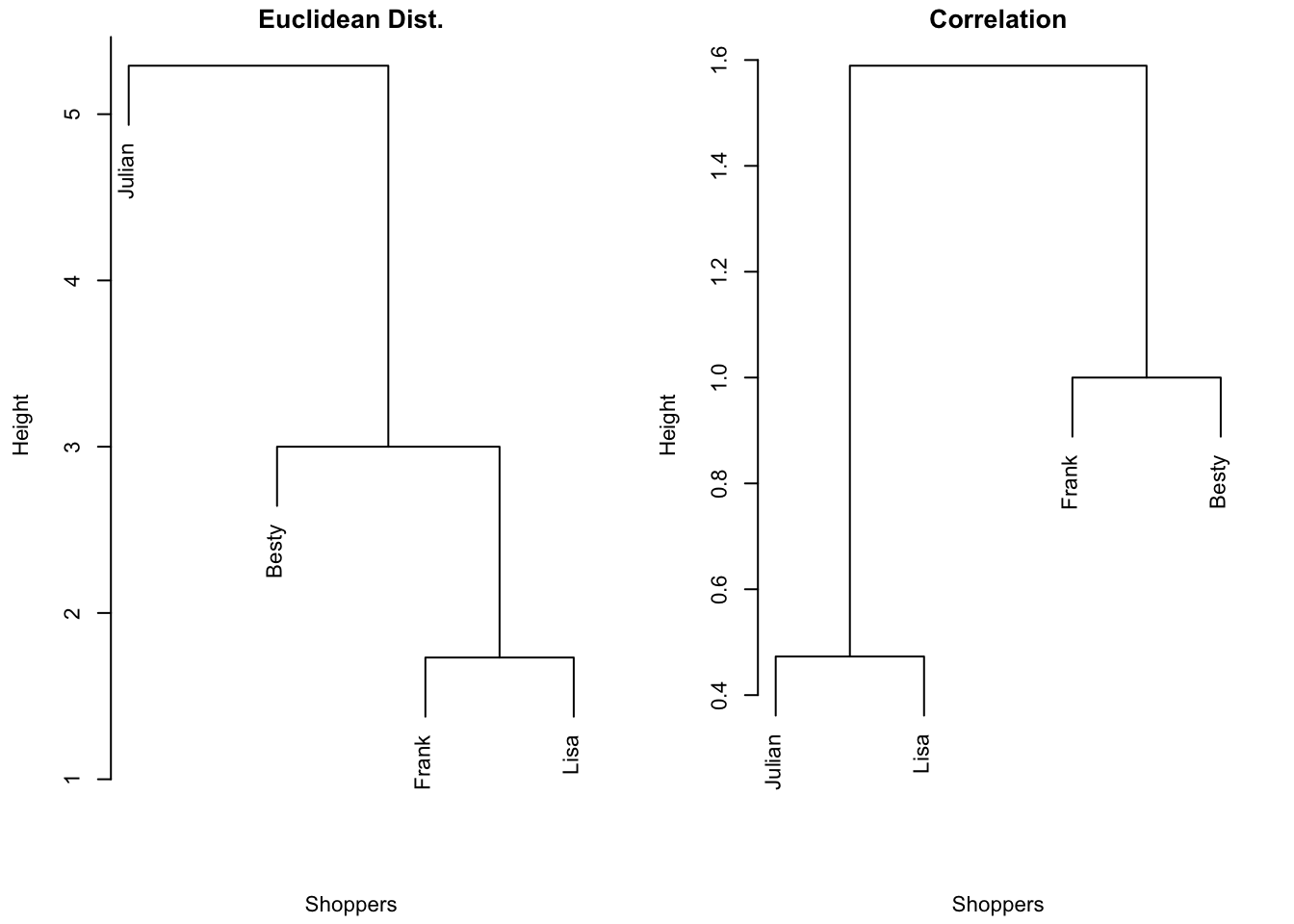
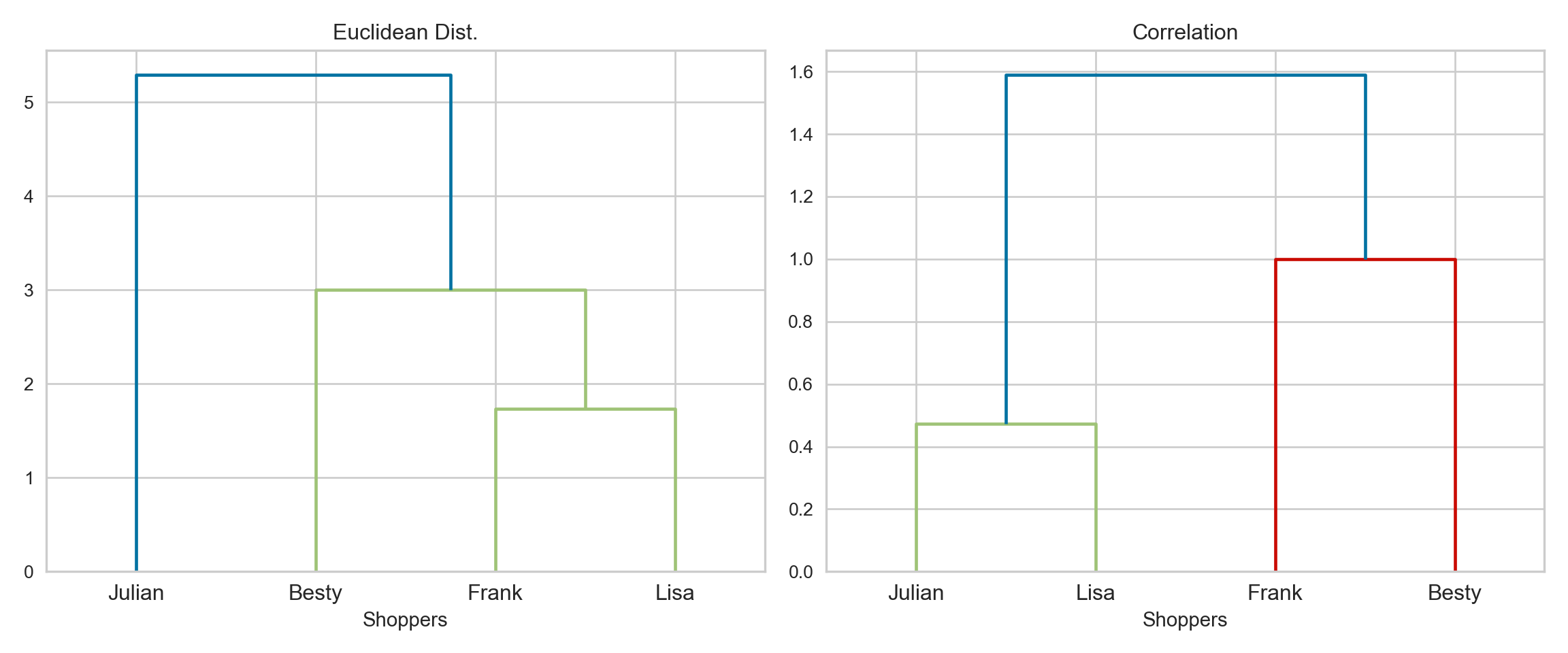
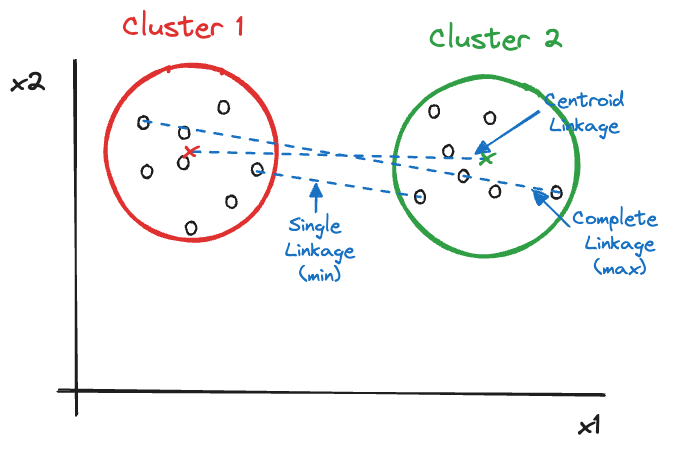
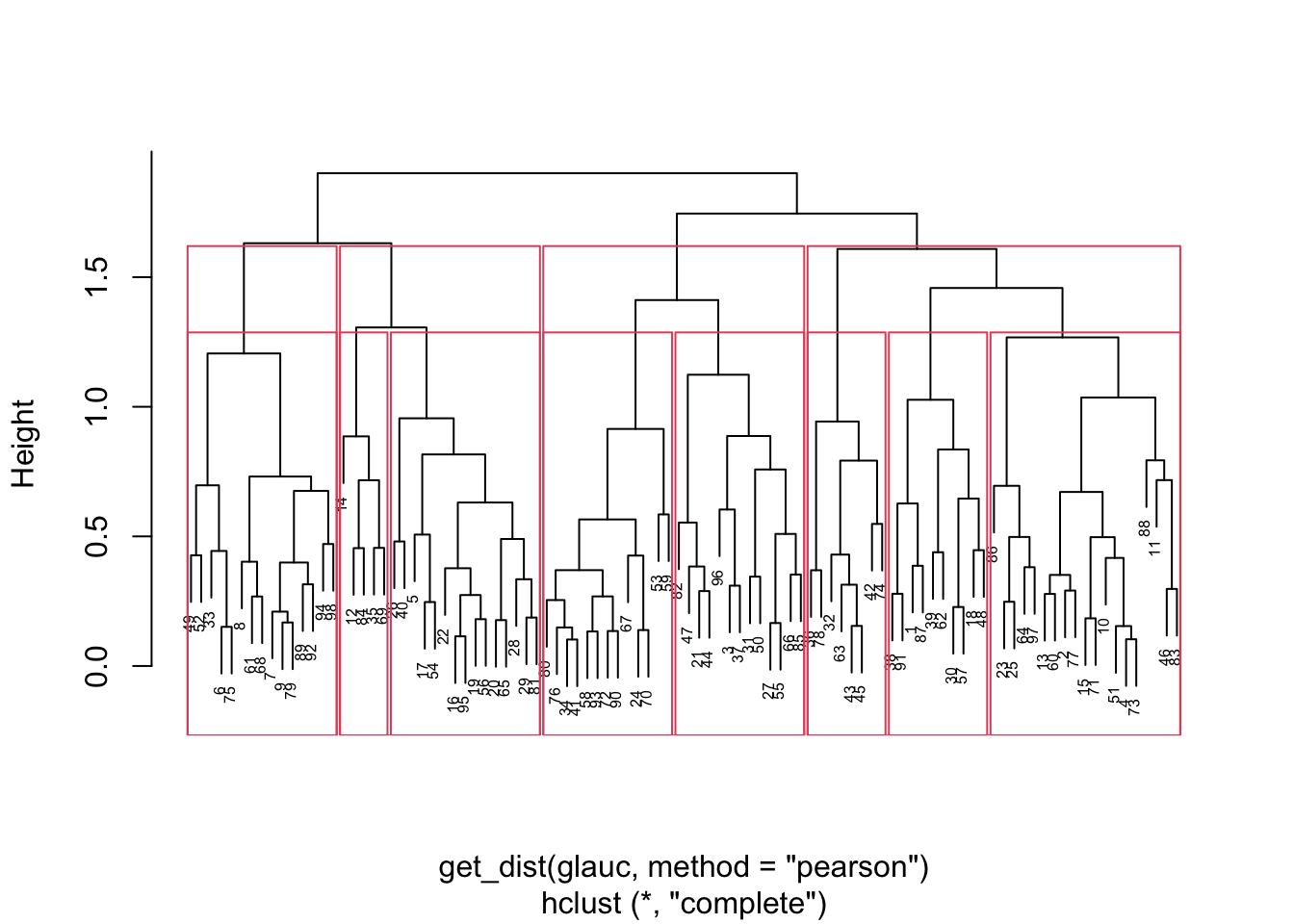
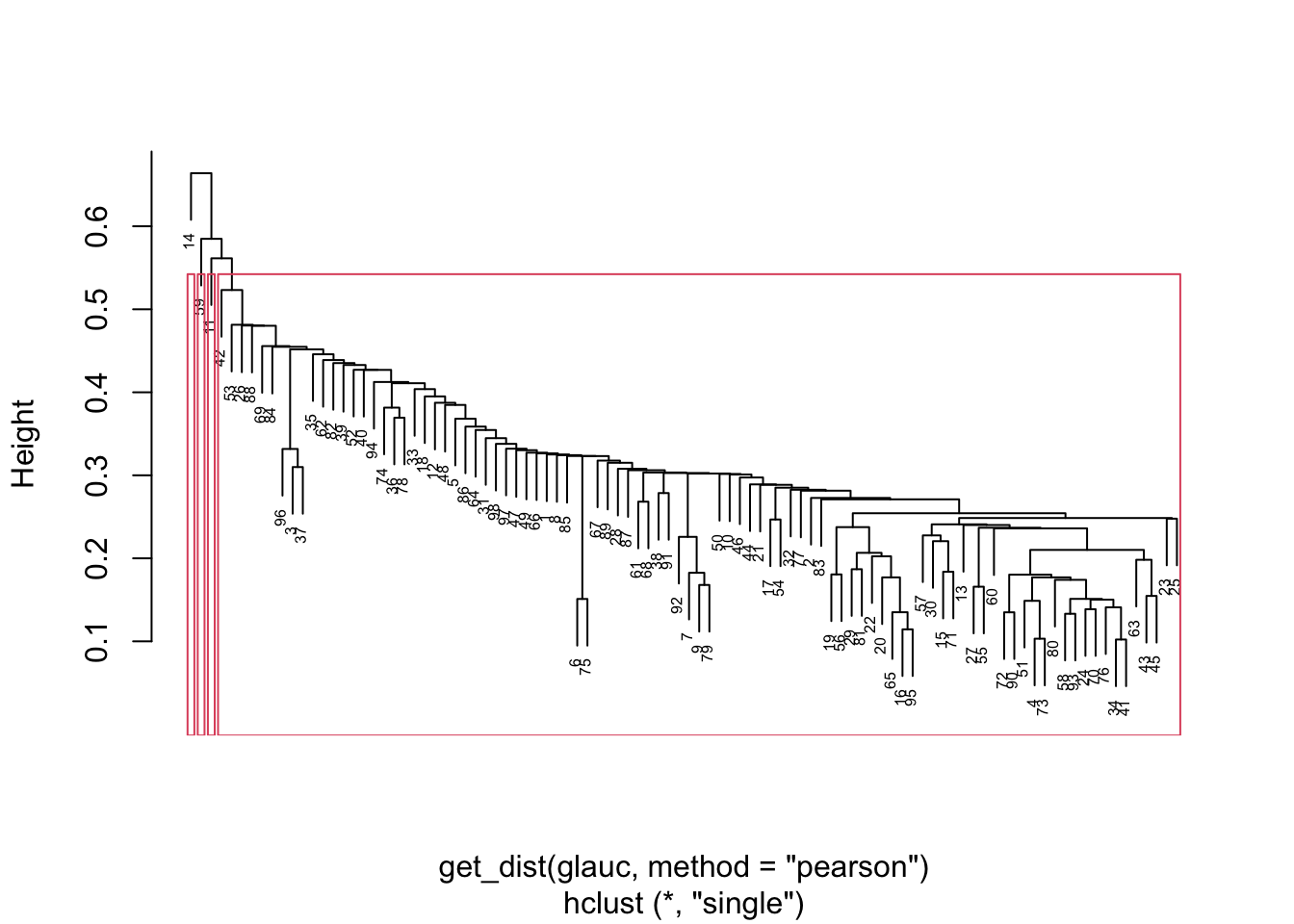
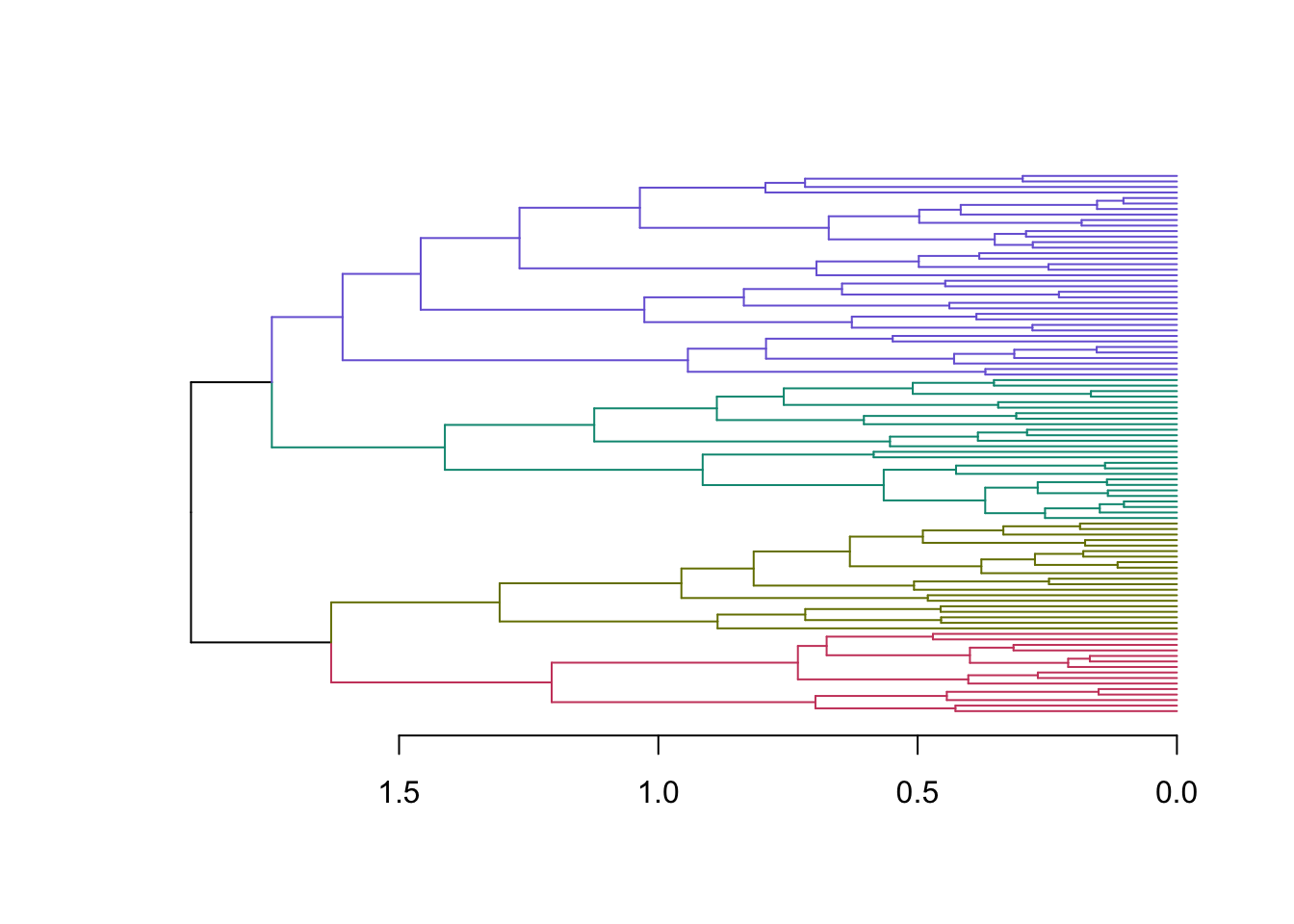
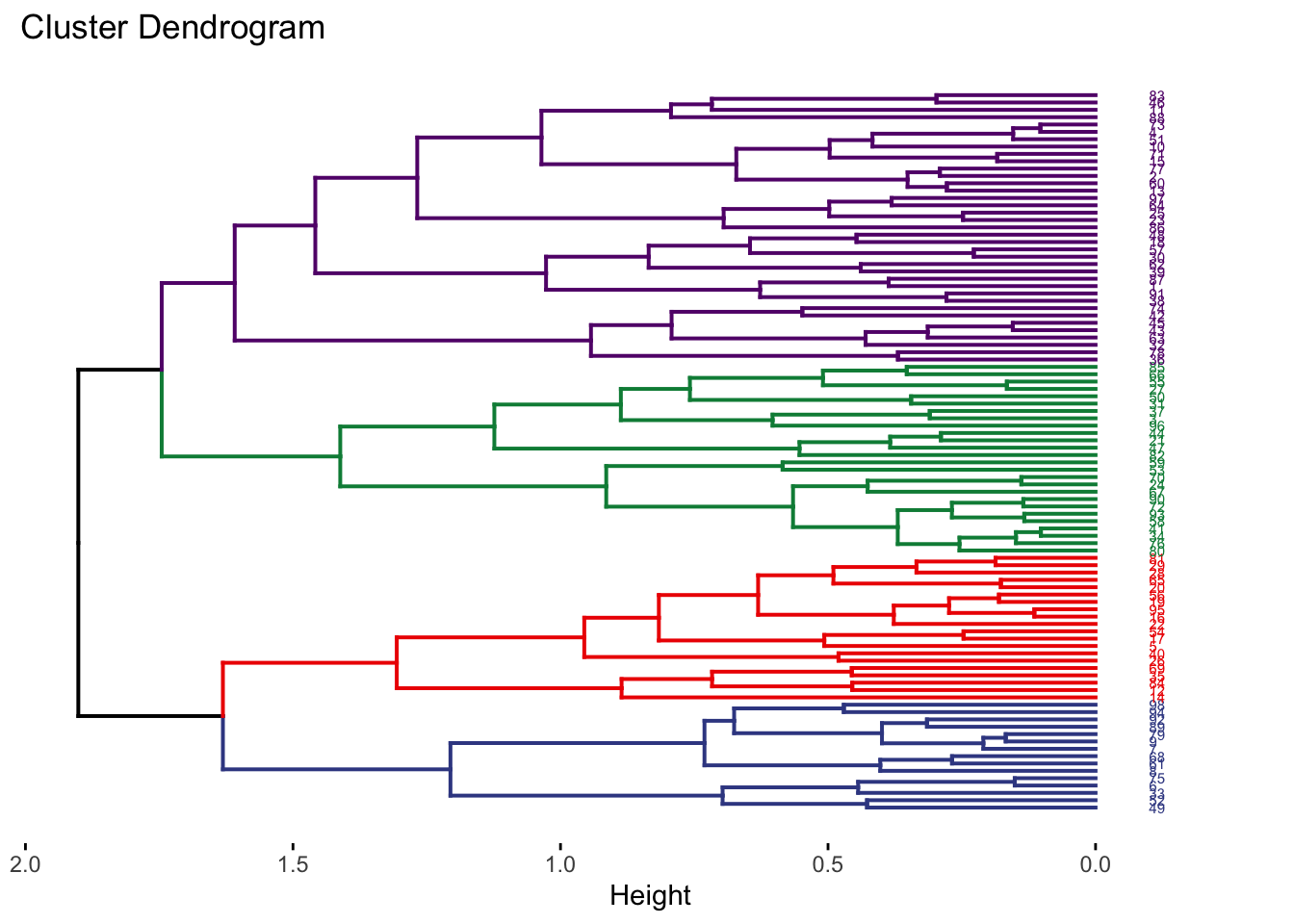
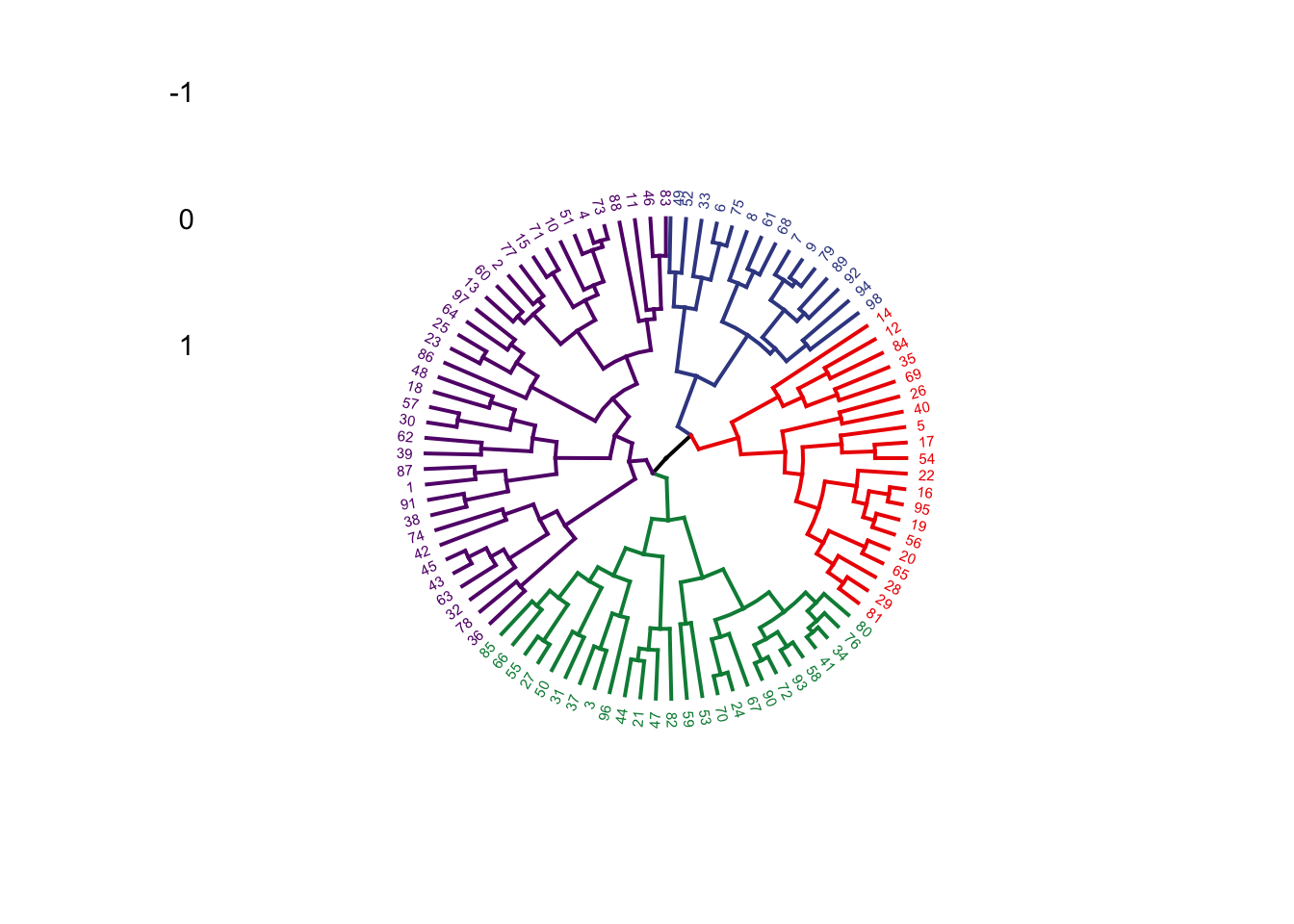
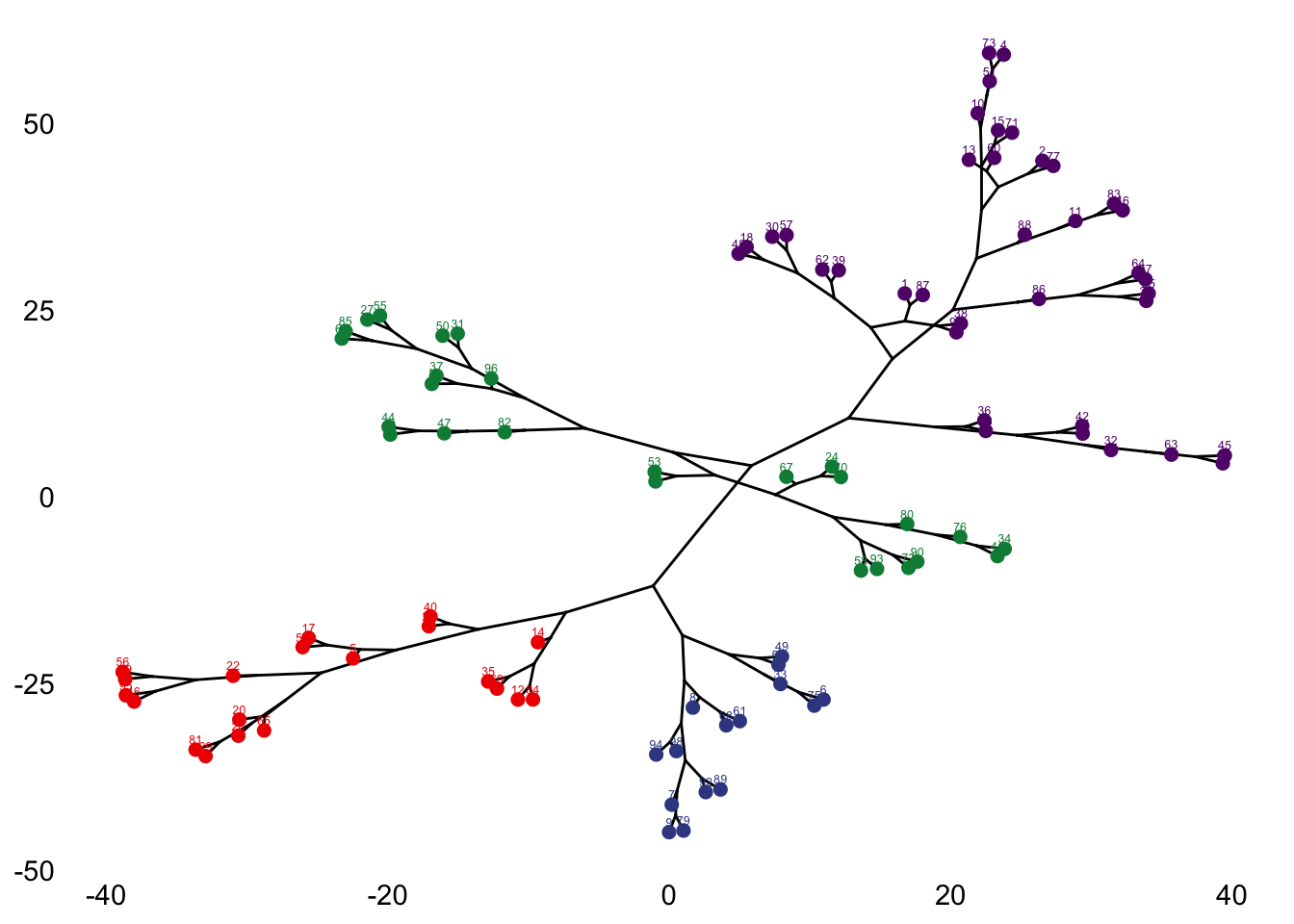
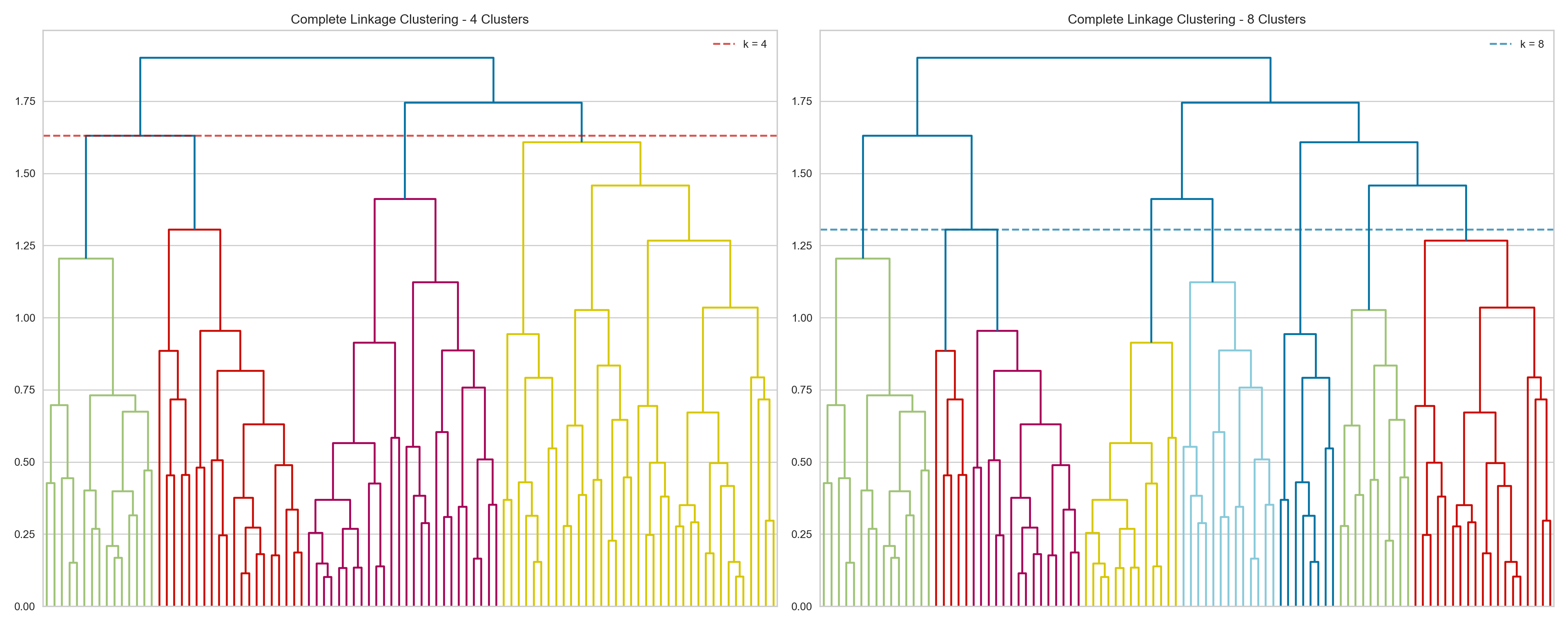
{'icoord': [[105.0, 105.0, 115.0, 115.0], [95.0, 95.0, 110.0, 110.0], [205.0, 205.0, 215.0, 215.0], [195.0, 195.0, 210.0, 210.0], [385.0, 385.0, 395.0, 395.0], [445.0, 445.0, 455.0, 455.0], [465.0, 465.0, 475.0, 475.0], [505.0, 505.0, 515.0, 515.0], [495.0, 495.0, 510.0, 510.0], [485.0, 485.0, 502.5, 502.5], [575.0, 575.0, 585.0, 585.0], [635.0, 635.0, 645.0, 645.0], [655.0, 655.0, 665.0, 665.0], [705.0, 705.0, 715.0, 715.0], [695.0, 695.0, 710.0, 710.0], [685.0, 685.0, 702.5, 702.5], [675.0, 675.0, 693.75, 693.75], [660.0, 660.0, 684.375, 684.375], [640.0, 640.0, 672.1875, 672.1875], [745.0, 745.0, 755.0, 755.0], [735.0, 735.0, 750.0, 750.0], [725.0, 725.0, 742.5, 742.5], [775.0, 775.0, 785.0, 785.0], [805.0, 805.0, 815.0, 815.0], [835.0, 835.0, 845.0, 845.0], [825.0, 825.0, 840.0, 840.0], [865.0, 865.0, 875.0, 875.0], [885.0, 885.0, 895.0, 895.0], [915.0, 915.0, 925.0, 925.0], [905.0, 905.0, 920.0, 920.0], [890.0, 890.0, 912.5, 912.5], [870.0, 870.0, 901.25, 901.25], [855.0, 855.0, 885.625, 885.625], [832.5, 832.5, 870.3125, 870.3125], [810.0, 810.0, 851.40625, 851.40625], [945.0, 945.0, 955.0, 955.0], [935.0, 935.0, 950.0, 950.0], [830.703125, 830.703125, 942.5, 942.5], [795.0, 795.0, 886.6015625, 886.6015625], [780.0, 780.0, 840.80078125, 840.80078125], [765.0, 765.0, 810.400390625, 810.400390625], [733.75, 733.75, 787.7001953125, 787.7001953125], [965.0, 965.0, 975.0, 975.0], [760.72509765625, 760.72509765625, 970.0, 970.0], [656.09375, 656.09375, 865.362548828125, 865.362548828125], [625.0, 625.0, 760.7281494140625, 760.7281494140625], [615.0, 615.0, 692.8640747070312, 692.8640747070312], [605.0, 605.0, 653.9320373535156, 653.9320373535156], [595.0, 595.0, 629.4660186767578, 629.4660186767578], [580.0, 580.0, 612.2330093383789, 612.2330093383789], [565.0, 565.0, 596.1165046691895, 596.1165046691895], [555.0, 555.0, 580.5582523345947, 580.5582523345947], [545.0, 545.0, 567.7791261672974, 567.7791261672974], [535.0, 535.0, 556.3895630836487, 556.3895630836487], [525.0, 525.0, 545.6947815418243, 545.6947815418243], [493.75, 493.75, 535.3473907709122, 535.3473907709122], [470.0, 470.0, 514.5486953854561, 514.5486953854561], [450.0, 450.0, 492.27434769272804, 492.27434769272804], [435.0, 435.0, 471.137173846364, 471.137173846364], [425.0, 425.0, 453.068586923182, 453.068586923182], [415.0, 415.0, 439.034293461591, 439.034293461591], [405.0, 405.0, 427.0171467307955, 427.0171467307955], [390.0, 390.0, 416.00857336539775, 416.00857336539775], [375.0, 375.0, 403.0042866826989, 403.0042866826989], [365.0, 365.0, 389.00214334134944, 389.00214334134944], [355.0, 355.0, 377.0010716706747, 377.0010716706747], [345.0, 345.0, 366.00053583533736, 366.00053583533736], [335.0, 335.0, 355.5002679176687, 355.5002679176687], [325.0, 325.0, 345.25013395883434, 345.25013395883434], [315.0, 315.0, 335.12506697941717, 335.12506697941717], [305.0, 305.0, 325.0625334897086, 325.0625334897086], [295.0, 295.0, 315.0312667448543, 315.0312667448543], [285.0, 285.0, 305.01563337242715, 305.01563337242715], [275.0, 275.0, 295.0078166862136, 295.0078166862136], [265.0, 265.0, 285.0039083431068, 285.0039083431068], [255.0, 255.0, 275.0019541715534, 275.0019541715534], [245.0, 245.0, 265.0009770857767, 265.0009770857767], [235.0, 235.0, 255.00048854288835, 255.00048854288835], [225.0, 225.0, 245.00024427144416, 245.00024427144416], [202.5, 202.5, 235.00012213572208, 235.00012213572208], [185.0, 185.0, 218.75006106786105, 218.75006106786105], [175.0, 175.0, 201.87503053393053, 201.87503053393053], [165.0, 165.0, 188.43751526696525, 188.43751526696525], [155.0, 155.0, 176.71875763348262, 176.71875763348262], [145.0, 145.0, 165.8593788167413, 165.8593788167413], [135.0, 135.0, 155.42968940837065, 155.42968940837065], [125.0, 125.0, 145.21484470418534, 145.21484470418534], [102.5, 102.5, 135.10742235209267, 135.10742235209267], [85.0, 85.0, 118.80371117604633, 118.80371117604633], [75.0, 75.0, 101.90185558802317, 101.90185558802317], [65.0, 65.0, 88.45092779401159, 88.45092779401159], [55.0, 55.0, 76.7254638970058, 76.7254638970058], [45.0, 45.0, 65.8627319485029, 65.8627319485029], [35.0, 35.0, 55.43136597425145, 55.43136597425145], [25.0, 25.0, 45.215682987125724, 45.215682987125724], [15.0, 15.0, 35.10784149356286, 35.10784149356286], [5.0, 5.0, 25.05392074678143, 25.05392074678143]], 'dcoord': [[0.0, 0.3099301524369442, 0.3099301524369442, 0.0], [0.0, 0.33174938255125574, 0.33174938255125574, 0.3099301524369442], [0.0, 0.3693877054853454, 0.3693877054853454, 0.0], [0.0, 0.3815268540039486, 0.3815268540039486, 0.3693877054853454], [0.0, 0.15104361992729431, 0.15104361992729431, 0.0], [0.0, 0.26823084455493573, 0.26823084455493573, 0.0], [0.0, 0.27861147145671505, 0.27861147145671505, 0.0], [0.0, 0.16792694446987888, 0.16792694446987888, 0.0], [0.0, 0.18257423546727902, 0.18257423546727902, 0.16792694446987888], [0.0, 0.2258490647475634, 0.2258490647475634, 0.18257423546727902], [0.0, 0.2467681707548327, 0.2467681707548327, 0.0], [0.0, 0.1806036559929557, 0.1806036559929557, 0.0], [0.0, 0.1868671617993154, 0.1868671617993154, 0.0], [0.0, 0.11445126497486058, 0.11445126497486058, 0.0], [0.0, 0.13505381671550198, 0.13505381671550198, 0.11445126497486058], [0.0, 0.17703417628010532, 0.17703417628010532, 0.13505381671550198], [0.0, 0.20243273239203363, 0.20243273239203363, 0.17703417628010532], [0.1868671617993154, 0.20661697799784795, 0.20661697799784795, 0.20243273239203363], [0.1806036559929557, 0.23756464791100718, 0.23756464791100718, 0.20661697799784795], [0.0, 0.18382889623106247, 0.18382889623106247, 0.0], [0.0, 0.220664216174967, 0.220664216174967, 0.18382889623106247], [0.0, 0.2276110333377006, 0.2276110333377006, 0.220664216174967], [0.0, 0.165797232341662, 0.165797232341662, 0.0], [0.0, 0.13496879944580653, 0.13496879944580653, 0.0], [0.0, 0.10318232796894677, 0.10318232796894677, 0.0], [0.0, 0.1488020776622505, 0.1488020776622505, 0.10318232796894677], [0.0, 0.133192794622228, 0.133192794622228, 0.0], [0.0, 0.13869511933908607, 0.13869511933908607, 0.0], [0.0, 0.1022034166089496, 0.1022034166089496, 0.0], [0.0, 0.1409643255563786, 0.1409643255563786, 0.1022034166089496], [0.13869511933908607, 0.1502276607565718, 0.1502276607565718, 0.1409643255563786], [0.133192794622228, 0.15113664271650296, 0.15113664271650296, 0.1502276607565718], [0.0, 0.17408110729209758, 0.17408110729209758, 0.15113664271650296], [0.1488020776622505, 0.17706816402011438, 0.17706816402011438, 0.17408110729209758], [0.13496879944580653, 0.1803397904327696, 0.1803397904327696, 0.17706816402011438], [0.0, 0.15470254966203856, 0.15470254966203856, 0.0], [0.0, 0.1982430665762347, 0.1982430665762347, 0.15470254966203856], [0.1803397904327696, 0.21012977743424577, 0.21012977743424577, 0.1982430665762347], [0.0, 0.23608002937594696, 0.23608002937594696, 0.21012977743424577], [0.165797232341662, 0.2368338644552197, 0.2368338644552197, 0.23608002937594696], [0.0, 0.24012476974730945, 0.24012476974730945, 0.2368338644552197], [0.2276110333377006, 0.24093827716593985, 0.24093827716593985, 0.24012476974730945], [0.0, 0.2477664712095553, 0.2477664712095553, 0.0], [0.24093827716593985, 0.24854725894214147, 0.24854725894214147, 0.2477664712095553], [0.23756464791100718, 0.2542973948286472, 0.2542973948286472, 0.24854725894214147], [0.0, 0.27105407434018214, 0.27105407434018214, 0.2542973948286472], [0.0, 0.27273668637263004, 0.27273668637263004, 0.27105407434018214], [0.0, 0.28146719444854573, 0.28146719444854573, 0.27273668637263004], [0.0, 0.2825975306770947, 0.2825975306770947, 0.28146719444854573], [0.2467681707548327, 0.28506833272888843, 0.28506833272888843, 0.2825975306770947], [0.0, 0.2885295036052501, 0.2885295036052501, 0.28506833272888843], [0.0, 0.28905783121970086, 0.28905783121970086, 0.2885295036052501], [0.0, 0.2973906549190045, 0.2973906549190045, 0.28905783121970086], [0.0, 0.30098279161476127, 0.30098279161476127, 0.2973906549190045], [0.0, 0.30160961218139926, 0.30160961218139926, 0.30098279161476127], [0.2258490647475634, 0.3021538623099621, 0.3021538623099621, 0.30160961218139926], [0.27861147145671505, 0.30275367599477887, 0.30275367599477887, 0.3021538623099621], [0.26823084455493573, 0.3033802488056636, 0.3033802488056636, 0.30275367599477887], [0.0, 0.30612387313870826, 0.30612387313870826, 0.3033802488056636], [0.0, 0.30783161672865655, 0.30783161672865655, 0.30612387313870826], [0.0, 0.3150898386757859, 0.3150898386757859, 0.30783161672865655], [0.0, 0.31773714738541226, 0.31773714738541226, 0.3150898386757859], [0.15104361992729431, 0.32316608791290535, 0.32316608791290535, 0.31773714738541226], [0.0, 0.32327988904631766, 0.32327988904631766, 0.32316608791290535], [0.0, 0.32427952162875573, 0.32427952162875573, 0.32327988904631766], [0.0, 0.3250798867054798, 0.3250798867054798, 0.32427952162875573], [0.0, 0.32641894169923547, 0.32641894169923547, 0.3250798867054798], [0.0, 0.3272579781062841, 0.3272579781062841, 0.32641894169923547], [0.0, 0.3302518732988847, 0.3302518732988847, 0.3272579781062841], [0.0, 0.3320392697494122, 0.3320392697494122, 0.3302518732988847], [0.0, 0.337874834706127, 0.337874834706127, 0.3320392697494122], [0.0, 0.34474313802956214, 0.34474313802956214, 0.337874834706127], [0.0, 0.3545683960369016, 0.3545683960369016, 0.34474313802956214], [0.0, 0.3586806371194541, 0.3586806371194541, 0.3545683960369016], [0.0, 0.36815217064053063, 0.36815217064053063, 0.3586806371194541], [0.0, 0.3847804960259954, 0.3847804960259954, 0.36815217064053063], [0.0, 0.3873804376982909, 0.3873804376982909, 0.3847804960259954], [0.0, 0.39505358942269164, 0.39505358942269164, 0.3873804376982909], [0.0, 0.40381621801532186, 0.40381621801532186, 0.39505358942269164], [0.3815268540039486, 0.4109322593469308, 0.4109322593469308, 0.40381621801532186], [0.0, 0.4124175725502991, 0.4124175725502991, 0.4109322593469308], [0.0, 0.42697781781882405, 0.42697781781882405, 0.4124175725502991], [0.0, 0.427094947043108, 0.427094947043108, 0.42697781781882405], [0.0, 0.43287192471933145, 0.43287192471933145, 0.427094947043108], [0.0, 0.4351979477566871, 0.4351979477566871, 0.43287192471933145], [0.0, 0.43883296055112564, 0.43883296055112564, 0.4351979477566871], [0.0, 0.44580837966110376, 0.44580837966110376, 0.43883296055112564], [0.33174938255125574, 0.4516994506939689, 0.4516994506939689, 0.44580837966110376], [0.0, 0.4547810204336292, 0.4547810204336292, 0.4516994506939689], [0.0, 0.4556697381730924, 0.4556697381730924, 0.4547810204336292], [0.0, 0.48014032103944426, 0.48014032103944426, 0.4556697381730924], [0.0, 0.48039986445841887, 0.48039986445841887, 0.48014032103944426], [0.0, 0.48134341932384306, 0.48134341932384306, 0.48039986445841887], [0.0, 0.5231995673063781, 0.5231995673063781, 0.48134341932384306], [0.0, 0.5614024965006799, 0.5614024965006799, 0.5231995673063781], [0.0, 0.5848685297607765, 0.5848685297607765, 0.5614024965006799], [0.0, 0.6639624413005827, 0.6639624413005827, 0.5848685297607765]], 'ivl': ['13', '58', '10', '41', '52', '25', '87', '68', '83', '95', '2', '36', '34', '61', '81', '38', '51', '39', '93', '73', '35', '77', '32', '17', '11', '47', '4', '85', '63', '30', '97', '96', '46', '48', '65', '0', '7', '84', '5', '74', '66', '88', '27', '86', '60', '67', '37', '90', '91', '6', '8', '78', '49', '9', '45', '43', '20', '16', '53', '31', '76', '1', '82', '18', '55', '28', '80', '21', '19', '64', '15', '94', '56', '29', '14', '70', '12', '26', '54', '59', '71', '89', '50', '3', '72', '79', '57', '92', '23', '69', '75', '33', '40', '62', '42', '44', '22', '24'], 'leaves': [13, 58, 10, 41, 52, 25, 87, 68, 83, 95, 2, 36, 34, 61, 81, 38, 51, 39, 93, 73, 35, 77, 32, 17, 11, 47, 4, 85, 63, 30, 97, 96, 46, 48, 65, 0, 7, 84, 5, 74, 66, 88, 27, 86, 60, 67, 37, 90, 91, 6, 8, 78, 49, 9, 45, 43, 20, 16, 53, 31, 76, 1, 82, 18, 55, 28, 80, 21, 19, 64, 15, 94, 56, 29, 14, 70, 12, 26, 54, 59, 71, 89, 50, 3, 72, 79, 57, 92, 23, 69, 75, 33, 40, 62, 42, 44, 22, 24], 'color_list': ['C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C0', 'C0', 'C0'], 'leaves_color_list': ['C0', 'C0', 'C0', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1', 'C1']}