23  Introduction

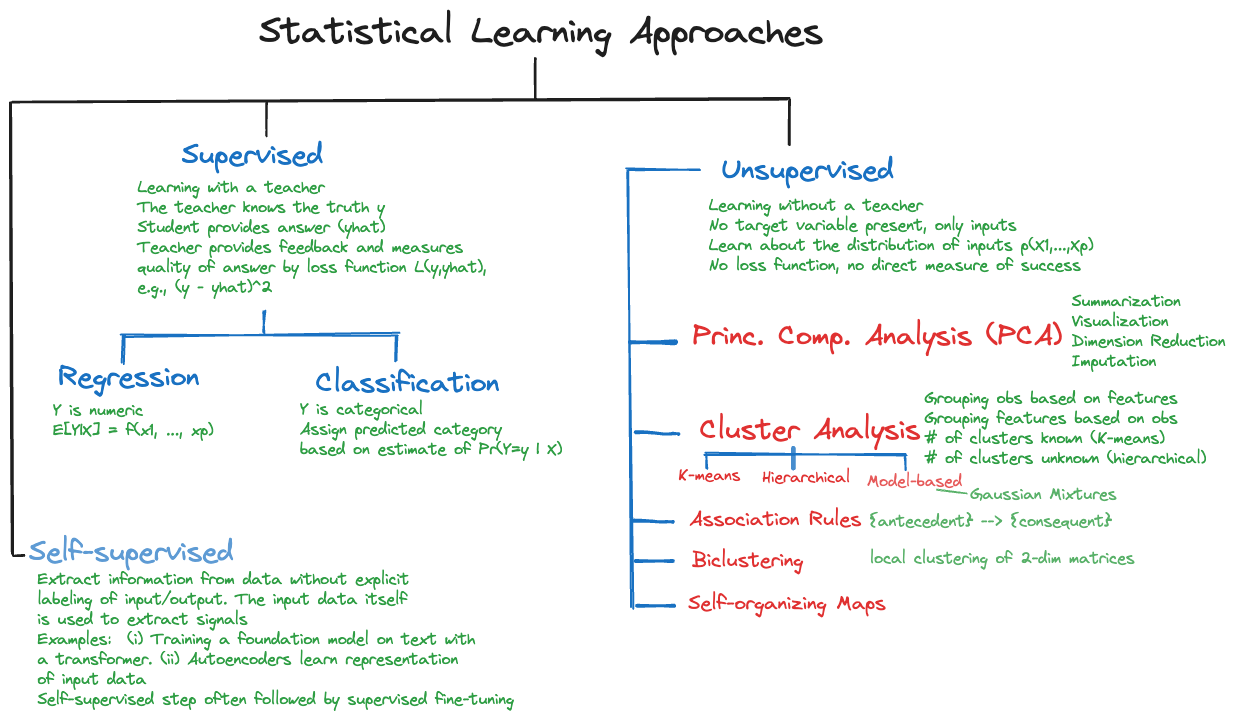
The methods discussed so far fall into the category of supervised learning, where a target variable \(Y\) is present and the goal is to predict or classify \(Y\) or to test hypothesis about \(Y\). The distinction between supervised and unsupervised methods of learning from data was introduced in Chapter 5.

Recall that the term unsupervised learning seeks to evoke learning without a teacher who can judge the quality of an answer because the teacher is aware of the correct answer, the ground truth. In unsupervised learning there are no loss functions and no clear metrics on how to evaluate the quality of the analysis. The proliferation of method of unsupervised learning and the reliance on heuristics are a result of this condition.

However, unsupervised learning is not a lesser form of learning from data and the questions it addresses can be more complex than estimating the mean of a random variable. In general, the data for unsupervised learning consists of \(n\) tuples \([X_1, \cdots, X_p]\); because there is no target variable, the data structure is also referred to as unlabeled data. We are interested in discovering aspects of the joint distribution \(p(X_1, \cdots, X_p) = p(\textbf{X})\) (Figure 23.1). For example,

Because there is no target variable, unsupervised methods of learning rely less on model structures and probabilistic assumptions–with some exceptions such as model-based clustering. The field has more of an exploratory nature than supervised learning; that makes it less confirmatory and maybe more fun. For example, there are no strict rules on how to perform a hierarchical cluster analysis and different analysts will create different cluster assignments. Finding the optimal number \(k\) in \(k\)-means clustering escapes cross-validation because there is no loss function according to which errors can be measured.